No matter how complex the system is, the basic building block of all computers is the binary number system, 1s and 0s. This system has been chosen due to the fact computers are made of millions of tine “switches” that either turn on or off (think about electricity) – this logically fits well with the binary number system. A 1 represents an ON switch, whereas a 0 represents an OFF switch.

A computer is a big ole’ pile of switches. Imagine an on/off switch connected to a bulb:
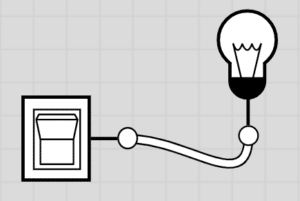
Now, imagine it’s connected to other switches and other bulbs:
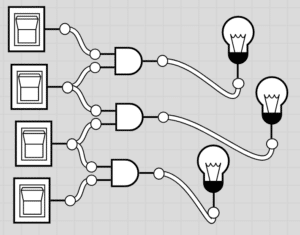
Advertisement
FInally, imagine a whole room covered in these switches and bulbs. that’s kind of like what a computer is. If we hit one certain switch, or a combination of them, it will turn on a specific bulb. You can imagine this like when you press the letter A on your keyboard, all of the different switches go into action in order to “light up” the correct bulb (such as the A appearing on your monitor) so you can write words on your documents. The “logic” behind how these switches work is where a computer scientist comes into play. Let’s now talk about the number system behind this logic.
The binary system
you’re probably familiar with is the denary (base 10) system. This uses multiples of 10
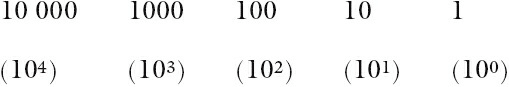
The BINARY SYSTEM is based on the number 2. Therefore, only the two ‘values’ 0 and 1 can be used to represent each digit. Using the same method as denary, this implies headings of 20, 21, 22, and so on. The typical headings for a binary number with eight digits would be:
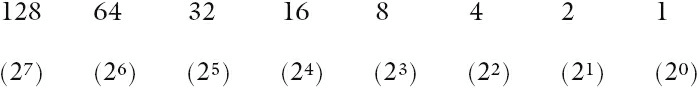
11101001 would be a typical binary number you may see.
Converting binary to denary
it’s quite simple, really. every time you see a “1” you should add the values together. Take a look:
128 + 64 + 32 + 8 + 1 = 233
Converting denary to binary
the reverse operation is a little different and more complex.
Method 1
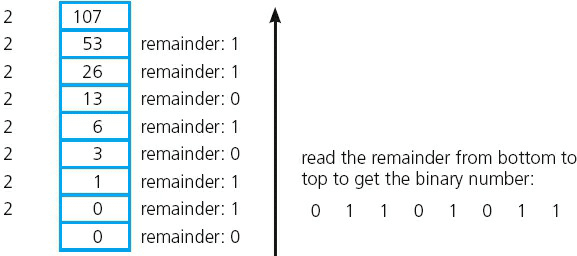
Consider the conversion of the denary number, 107, into binary. This method
involves placing 1s in the appropriate position so that the total equates to 107:
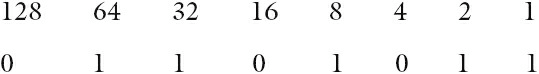
Method 2
This method involves successive division by 2. The remainders are then read from
BOTTOM to TOP to give the binary value. Again using 107, we get:
How do we measure computer memory?
A binary digit is a BIT; 8 bits is a BYTE. A byte is the smallest unit of memory in a computer (for example to represent the letter “A”). Some computers may use larger bytes but they are multiples of 8 (e.g. 32-bit systems). One byte of memory wouldn’t allow you to store very much, only a single number, character or pixel of an image; memory size is, therefore, measured like this:
1 kilobyte (1 KB) = 210 1 024 bytes
1 megabyte (1 MB) = 220 1 048 576 bytes
1 gigabyte (1 GB) = 230 1 073 741 824 bytes
1 terabyte (1 TB) = 240 1 099 511 627 776 bytes
1 petabyte (1 PB) = 250 1 125 899 906 842 624 bytes
Use cases for binary
Registers – this is covered in another topic under the “Systems Architecture” unit of work, however, registers are simply fast pieces of memory. An example of what it might look like:

We can use registers in controlling robots, for example. Each part of the robot is controlled by a different “register” which then consists of strings of binary numbers. This is how an 8-bit register might control a robot cleaner :

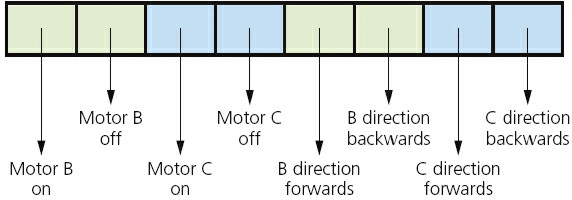
we can see that each “bit” would do something different in the system. The particular string of bits 10101001 above would, therefore, turn on motor B and C ON, it would then rotate B forwards and C backwards effectively turning the robot.
Test out your binary skills using this game!
