The Hexadecimal Number System and how to convert

Hexadecimal is another number system used by computers. They do not process hexadecimal but rather convert it to binary before processing it. To understand more about binary, check this post out. Hexadecimal (often referred to as simply ‘hex’) is a base 16 system and therefore needs to use 16 different ‘values’ to represent each digit. Because it is a system based on 16 different digits, the numbers 0 to 9 and the letters A to F are used to represent each hexadecimal (hex) digit. (A = 10, B = 11, C = 12, D = 13, E = 14 and F = 15.) Using the same method as denary and binary, this gives the headings of 160, 161, 162, 163 and so on. The typical headings for a hexadecimal number with five digits would be:

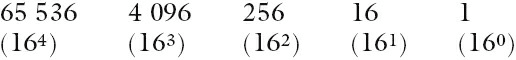
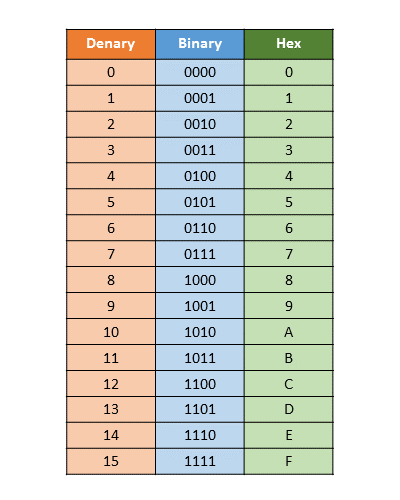
16 in binary is 2⁴ which means 4 bits are used for each hex digit. See the table below:

Converting from binary to hexadecimal

This is fairly easy. Starting from the right and moving left, split the binary number into groups of 4 bits. If the last group has less than 4 bits, then simply fill in with 0s from the left. Take each group of 4 bits and convert it into the equivalent hexadecimal digit using Table 1.2. Look at the following two examples to see how this works. This might look something like this:

Example 1

• 1 0 1 1 1 1 1 0 0 0 0 1

First, split this up into groups of 4 bits:

• 1 0 1 1 1 1 1 0 0 0 0 1

• B E 1

Example 2

• 1 0 0 0 0 1 1 1 1 1 1 1 0 1

split this into groups of 4 bits:

• 1 0 0 0 0 1 1 1 1 1 1 1 0 1

The left group only contains 2 bits, so add in two 0s:

• 0 0 1 0 0 0 0 1 1 1 1 1 1 1 0 1

Now use Table 1.2 to find the equivalent hexadecimal digits: 2 1 F D

Example 3 – Hex to Binary

• 4 F E 8

Using the table above, covert to groups of 4 bits

0100 1111 1110 1000

Put the bits together: 0100111111111000

Converting from hex to denary and denary to hex

This is not too bad. Take each digit and multiply by its place value.

Example: 4 5 A

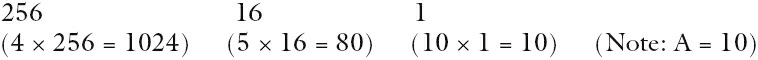
Add the totals – 1114

Therefore, 45A in denary is 1114

To convert from denary to hexadecimal is a little more difficult.

We can use the division by 16 method. Take the denary values, in this case 2004 and divide by 16. Each time writing down the remainder

• Step 1: 2004 / 16 = 125.25 (keep the 125 and work out the remainder)

You must then multiple the .25 by 16 to get the remainder 4 (unless you can work it out as a remainder in your head!). We continue to divide the integer number.

• Step 2: .25 * 16 = 4
• Step 3: 125 / 16 = 7.8125 (keep the 7 and work out the remainder
• Step 4: .8125 * 16 = 13
• Step 5: 7 cannot be divided by 16 so we just write “7” – now go from the bottom up and put everything together. See the illustration below

Therefore, 2004 in hexadecimal = 7 D 4

Why do we use hexademical?

Here are some uses for hexadecimal values in our computer systems.

Memory Dumps

hexadecimal is often used when developing new software or when trying to trace errors in programs.

B 5 A 4 1 A F C is much easier to work with than: 1 0 1 1 | 1 0 0 1 | 1 0 1 0 | 0 1 0 0 | 0 0 0 1 | 1 0 1 0 | 1 1 1 1 | 1 1 0 0

A developer can look at each of the hexadecimal codes (shown above) and find where the error lies.

Machine Code and Assembly Code

Computer memory can be referred to directly using machine or assembly code. This has several advantages. In the image below you can see how the different types of code compare to each other and how using Hexadecimal in the machine or assembly language can make things much easier to read than a sea of 1s and 0s.

Colour Codes in HTML/CSS

HYPERTEXT MARK-UP LANGUAGE (HTML) is used when writing and developing web pages. HTML isn’t a programming language but is simply a mark-up language used in the processing, definition and presentation of text. Here is a short section of HTML code:

<tr>
<td><h3>Small car</h3>
<h3>Used car sales</h3>
<h2>Cars from $500</h2>
<br><h2>Cash sales only</h2></td></br>
</tr>
<table border="1">
<colgroup>
<col span="2" style="background-color:red">
<col style="background-color:yellow">
</colgroup>

• # FF 00 00 represents primary colour red
• # 00 FF 00 represents primary colour green
• # 00 00 FF represents primary colour blue
• # FF 00 FF represents fuchsia
• # FF 80 00 represents orange
• # B1 89 04 represents tan

Media Access Control (MAC)

A MEDIA ACCESS CONTROL (MAC) ADDRESS refers to a number which uniquely identifies a device on the internet. The MAC address refers to the physical network interface card (NIC) which is part of the device. Because it is tied to your physical hardware it rarely changes, but it is possible!

A MAC address is usually made up of 48 bits which are shown as six groups of
hexadecimal digits (although 64-bit addresses are also known):

NN – NN – NN – DD – DD – DD or NN:NN:NN:DD:DD:DD

Web Addresses

ASCII is also used – this is known as the AMERICAN STANDARD CODE FOR INFORMATION INTERCHANGE. The codes can be represented by Hexadecimal as seen below:

That’s all for now, next is how computers can represent different types of files on our computers!